13.3 The Ideal Gas Law

OpenStax

95 13.3 The Ideal Gas Law

Summary

State the ideal gas law in terms of molecules and in terms of moles.
Use the ideal gas law to calculate pressure change, temperature change, volume change, or the number of molecules or moles in a given volume.
Use Avogadro’s number to convert between number of molecules and number of moles.

**Figure 1.** The air inside this hot air balloon flying over Putrajaya, Malaysia, is hotter than the ambient air. As a result, the balloon experiences a buoyant force pushing it upward. (credit: Kevin Poh, Flickr)

In this section, we continue to explore the thermal behavior of gases. In particular, we examine the characteristics of atoms and molecules that compose gases. (Most gases, for example nitrogen, $N_{2},$ and oxygen, $O_{2},$ are composed of two or more atoms. We will primarily use the term “molecule” in discussing a gas because the term can also be applied to monatomic gases, such as helium.)

Gases are easily compressed. We can see evidence of this in [link], where you will note that gases have the largest coefficients of volume expansion. The large coefficients mean that gases expand and contract very rapidly with temperature changes. In addition, you will note that most gases expand at the same rate, or have the same $β .$ This raises the question as to why gases should all act in nearly the same way, when liquids and solids have widely varying expansion rates.

The answer lies in the large separation of atoms and molecules in gases, compared to their sizes, as illustrated in Figure 2. Because atoms and molecules have large separations, forces between them can be ignored, except when they collide with each other during collisions. The motion of atoms and molecules (at temperatures well above the boiling temperature) is fast, such that the gas occupies all of the accessible volume and the expansion of gases is rapid. In contrast, in liquids and solids, atoms and molecules are closer together and are quite sensitive to the forces between them.

Spheres representing atoms and molecules; the spheres are relatively far apart and are distributed randomly. — **Figure 2.** Atoms and molecules in a gas are typically widely separated, as shown. Because the forces between them are quite weak at these distances, the properties of a gas depend more on the number of atoms per unit volume and on temperature than on the type of atom.

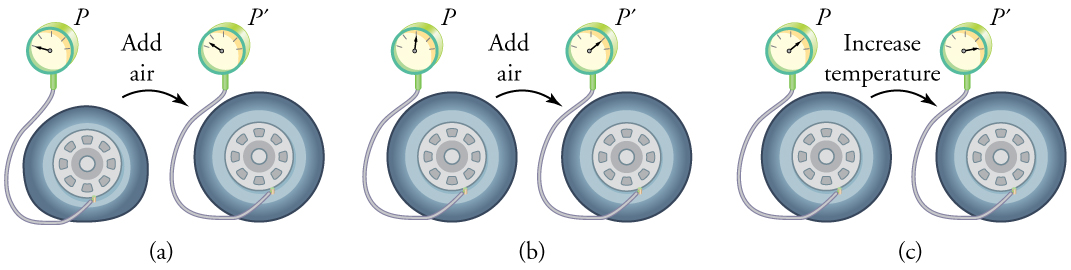
To get some idea of how pressure, temperature, and volume of a gas are related to one another, consider what happens when you pump air into an initially deflated tire. The tire’s volume first increases in direct proportion to the amount of air injected, without much increase in the tire pressure. Once the tire has expanded to nearly its full size, the walls limit volume expansion. If we continue to pump air into it, the pressure increases. The pressure will further increase when the car is driven and the tires move. Most manufacturers specify optimal tire pressure for cold tires. (See Figure 3.)

The figure has three parts, each part showing a pair of tires, and each tire connected to a pressure gauge. Each pair of tires represents the before and after images of a single tire, along with a change in pressure in that tire. In part a, the tire pressure is initially zero. After some air is added, represented by an arrow labeled Add air, the pressure rises to slightly above zero. In part b, the tire pressure is initially at the half-way mark. After some air is added, represented by an arrow labeled Add air, the pressure rises to the three-fourths mark. In part c, the tire pressure is initially at the three-fourths mark. After the temperature is raised, represented by an arrow labeled Increase temperature, the pressure rises to nearly the full mark. — **Figure 3.** (a) When air is pumped into a deflated tire, its volume first increases without much increase in pressure. (b) When the tire is filled to a certain point, the tire walls resist further expansion and the pressure increases with more air. (c) Once the tire is inflated, its pressure increases with temperature.

At room temperatures, collisions between atoms and molecules can be ignored. In this case, the gas is called an ideal gas, in which case the relationship between the pressure, volume, and temperature is given by the equation of state called the ideal gas law.

IDEAL GAS LAW

The ideal gas law states that

P V = N k T,

where $P$ is the absolute pressure of a gas, $V$ is the volume it occupies, $N$ is the number of atoms and molecules in the gas, and $T$ is its absolute temperature. The constant $k$ is called the Boltzmann constant in honor of Austrian physicist Ludwig Boltzmann (1844–1906) and has the value

k = 1.38 \times 10^{- 23} J/K .

The ideal gas law can be derived from basic principles, but was originally deduced from experimental measurements of Charles’ law (that volume occupied by a gas is proportional to temperature at a fixed pressure) and from Boyle’s law (that for a fixed temperature, the product $P V$ is a constant). In the ideal gas model, the volume occupied by its atoms and molecules is a negligible fraction of $V .$ The ideal gas law describes the behavior of real gases under most conditions. (Note, for example, that $N$ is the total number of atoms and molecules, independent of the type of gas.)

Let us see how the ideal gas law is consistent with the behavior of filling the tire when it is pumped slowly and the temperature is constant. At first, the pressure $P$ is essentially equal to atmospheric pressure, and the volume $V$ increases in direct proportion to the number of atoms and molecules $N$ put into the tire. Once the volume of the tire is constant, the equation $P V = N k T$ predicts that the pressure should increase in proportion to the number N of atoms and molecules.

Example 1: Calculating Pressure Changes Due to Temperature Changes: Tire Pressure

Suppose your bicycle tire is fully inflated, with an absolute pressure of $7.00 \times 10^{5} Pa$ (a gauge pressure of just under $90.0 {lb/in}^{2}$ ) at a temperature of ${18.0}^{0} C .$ What is the pressure after its temperature has risen to ${35.0}^{0} C ?$ Assume that there are no appreciable leaks or changes in volume.

Strategy

The pressure in the tire is changing only because of changes in temperature. First we need to identify what we know and what we want to know, and then identify an equation to solve for the unknown.

We know the initial pressure $P_{0} = 7.00 \times 10^{5} Pa,$ the initial temperature $T_{0} = {18.0}^{0} C,$ and the final temperature $T_{f} = {35.0}^{0} C .$ We must find the final pressure $P_{f} .$ How can we use the equation $P V = N k T ?$ At first, it may seem that not enough information is given, because the volume $V$ and number of atoms $N$ are not specified. What we can do is use the equation twice: $P_{0} V_{0} = N k T_{0}$ and $P_{f} V_{f} = N k T_{f} .$ If we divide $P_{f} V_{f}$ by $P_{0} V_{0}$ we can come up with an equation that allows us to solve for $P_{f} .$

\frac{P_{f} V_{f}}{P_{0} V_{0}}

=

\frac{N_{f} k T_{f}}{N_{0} k T_{0}}

Since the volume is constant, $V_{f}$ and $V_{0}$ are the same and they cancel out. The same is true for $N_{f}$ and $N_{0},$ and $k,$ which is a constant. Therefore,

\frac{P_{f}}{P_{0}}

=

\frac{T_{f}}{T_{0}} .

We can then rearrange this to solve for $P_{f} :$

P_{f} = P_{0}

\frac{T_{f}}{T_{0}},

where the temperature must be in units of kelvins, because $T_{0}$ and $T_{f}$ are absolute temperatures.

Solution

1. Convert temperatures from Celsius to Kelvin.

\begin{array}{l} T_{0} = (18.0 + 273) K = 291 K \\ T_{f} = (35.0 + 273) K = 308 K \end{array}

2. Substitute the known values into the equation.

P_{f} = P_{0}

\frac{T_{f}}{T_{0}}

= 7.00 \times 10^{5} Pa

(\frac{308 K}{291 K})

= 7.41 \times 10^{5} Pa

Discussion

The final temperature is about 6% greater than the original temperature, so the final pressure is about 6% greater as well. Note that absolute pressure and absolute temperature must be used in the ideal gas law.

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT—REFRIGERATING A BALLOON

Inflate a balloon at room temperature. Leave the inflated balloon in the refrigerator overnight. What happens to the balloon, and why?

Example 2: Calculating the Number of Molecules in a Cubic Meter of Gas

How many molecules are in a typical object, such as gas in a tire or water in a drink? We can use the ideal gas law to give us an idea of how large $N$ typically is.

Calculate the number of molecules in a cubic meter of gas at standard temperature and pressure (STP), which is defined to be $0^{0} C$ and atmospheric pressure.

Strategy

Because pressure, volume, and temperature are all specified, we can use the ideal gas law $P V = N k T,$ to find $N .$

Solution

1. Identify the knowns.

\begin{array}{l} T = 0^{0} C = 273 K \\ P = 1.01 \times 10^{5} Pa \\ V = 1.00 m^{3} \\ k = 1.38 \times 10^{- 23} J/K \end{array}

2. Identify the unknown: number of molecules, $N .$

3. Rearrange the ideal gas law to solve for $N .$

\begin{matrix} P V = N k T \\ N = \frac{P V}{k T} \end{matrix}

4. Substitute the known values into the equation and solve for $N .$

N =

\frac{P V}{k T}

=

\frac{(1.01 \times 10^{5} Pa) (1.00 m^{3})}{(31.38 \times 10^{- 23} J/K) (273 K)}

= 2.68 \times 10^{25} molecules

Discussion

This number is undeniably large, considering that a gas is mostly empty space. $N$ is huge, even in small volumes. For example, $1 {cm}^{3}$ of a gas at STP has $2.68 \times 10^{19}$ molecules in it. Once again, note that $N$ is the same for all types or mixtures of gases.

Moles and Avogadro’s Number

It is sometimes convenient to work with a unit other than molecules when measuring the amount of substance. A mole (abbreviated mol) is defined to be the amount of a substance that contains as many atoms or molecules as there are atoms in exactly 12 grams (0.012 kg) of carbon-12. The actual number of atoms or molecules in one mole is called Avogadro’s number $(N_{A}),$ in recognition of Italian scientist Amedeo Avogadro (1776–1856). He developed the concept of the mole, based on the hypothesis that equal volumes of gas, at the same pressure and temperature, contain equal numbers of molecules. That is, the number is independent of the type of gas. This hypothesis has been confirmed, and the value of Avogadro’s number is

N_{A} = 6.02 \times 10^{23} {mol}^{- 1} .

AVOGADRO’S NUMBER

One mole always contains $6.02 \times 10^{23}$ particles (atoms or molecules), independent of the element or substance. A mole of any substance has a mass in grams equal to its molecular mass, which can be calculated from the atomic masses given in the periodic table of elements.

N_{A} = 6.02 \times 10^{23} {mol}^{- 1}

The illustration shows relatively flat land with a solitary mountain, labeled Mt. Everest, and blue sky above. A double-headed vertical arrow stretches between the land and a point in the sky that is well above the peak of the mountain. The arrow, labeled table tennis balls, serves to indicate that a column of one mole of table tennis balls would reach a point in the sky that is much higher than the peak of Mt. Everest. — **Figure 4.** How big is a mole? On a macroscopic level, one mole of table tennis balls would cover the Earth to a depth of about 40 km.

Check Your Understanding 1

The active ingredient in a Tylenol pill is 325 mg of acetaminophen $(C_{8} H_{9} {NO}_{2}) .$ Find the number of active molecules of acetaminophen in a single pill.

Example 3: Calculating Moles per Cubic Meter and Liters per Mole

Calculate: (a) the number of moles in $1.00 m^{3}$ of gas at STP, and (b) the number of liters of gas per mole.

Strategy and Solution

(a) We are asked to find the number of moles per cubic meter, and we know from Example 2 that the number of molecules per cubic meter at STP is $2.68 \times 10^{25} .$ The number of moles can be found by dividing the number of molecules by Avogadro’s number. We let $n$ stand for the number of moles,

n {mol/m}^{3} =

\frac{N {molecules/m}^{3}}{6.02 \times 10^{23} molecules/mol}

=

\frac{2.68 \times 10^{25} {molecules/m}^{3}}{6.02 \times 10^{23} molecules/mol}

= 44.5 {mol/m}^{3} .

(b) Using the value obtained for the number of moles in a cubic meter, and converting cubic meters to liters, we obtain

\frac{(10^{3} {L/m}^{3})}{44.5 {mol/m}^{3}}

= 22.5 L/mol .

Discussion

This value is very close to the accepted value of 22.4 L/mol. The slight difference is due to rounding errors caused by using three-digit input. Again this number is the same for all gases. In other words, it is independent of the gas.

The (average) molar weight of air (approximately 80% $N_{2}$ and 20% $O_{2}$ is $M = 28.8 g .$ Thus the mass of one cubic meter of air is 1.28 kg. If a living room has dimensions $5 m \times 5 m \times 3 m,$ the mass of air inside the room is 96 kg, which is the typical mass of a human.

Check Your Understanding 2

The density of air at standard conditions $(P = 1 atm$ and $T = 20^{0} C)$ is $1.28 {kg/m}^{3} .$ At what pressure is the density $0.64 {kg/m}^{3}$ if the temperature and number of molecules are kept constant?

The Ideal Gas Law Restated Using Moles

A very common expression of the ideal gas law uses the number of moles, $n,$ rather than the number of atoms and molecules, $N .$ We start from the ideal gas law,

P V = N k T,

and multiply and divide the equation by Avogadro’s number $N_{A} .$ This gives

P V =

\frac{N}{N_{A}}

N_{A} k T .

Note that $n = N / N_{A}$ is the number of moles. We define the universal gas constant $R = N_{A} k,$ and obtain the ideal gas law in terms of moles.

IDEAL GAS LAW (IN TERMS OF MOLES)

The ideal gas law (in terms of moles) is

P V = n R T .

The numerical value of $R$ in SI units is

R = N_{A} k = (6.02 \times 10^{23} {mol}^{- 1}) (1.38 \times 10^{- 23} J/K) = 8.31 J/mol \cdot K .

In other units,

\begin{array}{l} R = 1.99 cal/mol \cdot K \\ R = 0.0821 L \cdot atm/mol \cdot K . \end{array}

You can use whichever value of $R$ is most convenient for a particular problem.

Example 4: Calculating Number of Moles: Gas in a Bike Tire

How many moles of gas are in a bike tire with a volume of $2.00 \times 10^{- 3} m^{3} (2.00 L)$ a pressure of $7.00 \times 10^{5} Pa$ (a gauge pressure of just under $90.0 {lb/in}^{2}$ ), and at a temperature of ${18.0}^{0} C ?$

Strategy

Identify the knowns and unknowns, and choose an equation to solve for the unknown. In this case, we solve the ideal gas law, $P V = n R T,$ for the number of moles $n .$

Solution

1. Identify the knowns.

\begin{array}{l} P = 7.00 \times 10^{5} Pa \\ V = 2.00 \times 10^{- 3} m^{3} \\ T = {18.0}^{0} C = 291 K \\ R = 8.31 J/mol \cdot K \end{array}

2. Rearrange the equation to solve for $n$ and substitute known values.

\begin{array}{lcl} n & = & \frac{P V}{R T} = \frac{(7.00 \times 10^{5} Pa) (2.00 \times 10^{- 3} m^{3})}{(8.31 J/mol \cdot K) (291 K)} \\ = & 0.579 mol \end{array}

Discussion

The most convenient choice for $R$ in this case is $8.31 J/mol \cdot K,$ because our known quantities are in SI units. The pressure and temperature are obtained from the initial conditions in Example 1, but we would get the same answer if we used the final values.

The ideal gas law can be considered to be another manifestation of the law of conservation of energy (see Chapter 7.6 Conservation of Energy). Work done on a gas results in an increase in its energy, increasing pressure and/or temperature, or decreasing volume. This increased energy can also be viewed as increased internal kinetic energy, given the gas’s atoms and molecules.

The Ideal Gas Law and Energy

Let us now examine the role of energy in the behavior of gases. When you inflate a bike tire by hand, you do work by repeatedly exerting a force through a distance. This energy goes into increasing the pressure of air inside the tire and increasing the temperature of the pump and the air.

The ideal gas law is closely related to energy: the units on both sides are joules. The right-hand side of the ideal gas law in $P V = N k T$ is $N k T .$ This term is roughly the amount of translational kinetic energy of $N$ atoms or molecules at an absolute temperature $T,$ as we shall see formally in Chapter 13.4 Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature. The left-hand side of the ideal gas law is $P V,$ which also has the units of joules. We know from our study of fluids that pressure is one type of potential energy per unit volume, so pressure multiplied by volume is energy. The important point is that there is energy in a gas related to both its pressure and its volume. The energy can be changed when the gas is doing work as it expands—something we explore in Chapter 14 Heat and Heat Transfer Methods—similar to what occurs in gasoline or steam engines and turbines.

PROBLEM-SOLVING STRATEGY: THE IDEAL GAS LAW

Step 1 Examine the situation to determine that an ideal gas is involved. Most gases are nearly ideal.

Step 2 Make a list of what quantities are given, or can be inferred from the problem as stated (identify the known quantities). Convert known values into proper SI units (K for temperature, Pa for pressure, $m^{3}$ for volume, molecules for $N,$ and moles for $n$ ).

Step 3 Identify exactly what needs to be determined in the problem (identify the unknown quantities). A written list is useful.

Step 4 Determine whether the number of molecules or the number of moles is known, in order to decide which form of the ideal gas law to use. The first form is $P V = N k T$ and involves $N,$ the number of atoms or molecules. The second form is $P V = n R T$ and involves $n,$ the number of moles.

Step 5 Solve the ideal gas law for the quantity to be determined (the unknown quantity). You may need to take a ratio of final states to initial states to eliminate the unknown quantities that are kept fixed.

Step 6 Substitute the known quantities, along with their units, into the appropriate equation, and obtain numerical solutions complete with units. Be certain to use absolute temperature and absolute pressure.

Step 7 Check the answer to see if it is reasonable: Does it make sense?

Check Your Understanding 3

Liquids and solids have densities about 1000 times greater than gases. Explain how this implies that the distances between atoms and molecules in gases are about 10 times greater than the size of their atoms and molecules.

Section Summary

The ideal gas law relates the pressure and volume of a gas to the number of gas molecules and the temperature of the gas.
The ideal gas law can be written in terms of the number of molecules of gas:
$P V = N k T,$

where $P$ is pressure, $V$ is volume, $T$ is temperature, $N$ is number of molecules, and $k$ is the Boltzmann constant

$k = 1.38 \times 10^{- 23} J/K .$
A mole is the number of atoms in a 12-g sample of carbon-12.
The number of molecules in a mole is called Avogadro’s number $N_{A},$
$N_{A} = 6.02 \times 10^{23} {mol}^{- 1} .$
A mole of any substance has a mass in grams equal to its molecular weight, which can be determined from the periodic table of elements.
The ideal gas law can also be written and solved in terms of the number of moles of gas:
$P V = n R T,$

where $n$ is number of moles and $R$ is the universal gas constant,

$R = 8.31 J/mol \cdot K .$
The ideal gas law is generally valid at temperatures well above the boiling temperature.

Conceptual Questions

1: Find out the human population of Earth. Is there a mole of people inhabiting Earth? If the average mass of a person is 60 kg, calculate the mass of a mole of people. How does the mass of a mole of people compare with the mass of Earth?

2: Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?

3: A constant-volume gas thermometer contains a fixed amount of gas. What property of the gas is measured to indicate its temperature?

Problems & Exercises

1: The gauge pressure in your car tires is $2.50 \times 10^{5} {N/m}^{2}$ at a temperature of ${35.0}^{0} C$ when you drive it onto a ferry boat to Alaska. What is their gauge pressure later, when their temperature has dropped to $- {40.0}^{0} C ?$

2: Convert an absolute pressure of $7.00 \times 10^{5} {N/m}^{2}$ to gauge pressure in ${lb/in}^{2} .$ (This value was stated to be just less than $90.0 {lb/in}^{2}$ in Example 4. Is it?)

3: Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of ${20.0}^{0} C .$ (a) Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is ${60.0}^{0} C$ (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks. (b) The actual final pressure for the light bulb will be less than calculated in part (a) because the glass bulb will expand. What will the actual final pressure be, taking this into account? Is this a negligible difference?

4: Large helium-filled balloons are used to lift scientific equipment to high altitudes. (a) What is the pressure inside such a balloon if it starts out at sea level with a temperature of ${10.0}^{0} C$ and rises to an altitude where its volume is twenty times the original volume and its temperature is $- {50.0}^{0} C ?$ (b) What is the gauge pressure? (Assume atmospheric pressure is constant.)

5: Confirm that the units of $n R T$ are those of energy for each value of $R :$ (a) $8.31 J/mol \cdot K,$ (b) $1.99 cal/mol \cdot K,$ and (c) $0.0821 L \cdot atm/mol \cdot K .$

6: In the text, it was shown that $N / V = 2.68 \times 10^{25} m^{- 3}$ for gas at STP. (a) Show that this quantity is equivalent to $N / V = 2.68 \times 10^{19} {cm}^{- 3},$ as stated. (b) About how many atoms are there in one $μ m^{3}$ (a cubic micrometer) at STP? (c) What does your answer to part (b) imply about the separation of atoms and molecules?

7: Calculate the number of moles in the 2.00-L volume of air in the lungs of the average person. Note that the air is at ${37.0}^{0} C$ (body temperature).

8: An airplane passenger has $100 {cm}^{3}$ of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to $7.50 \times 10^{4} {N/m}^{2} ?$

9: (a) What is the volume (in ${km}^{3}$ ) of Avogadro’s number of sand grains if each grain is a cube and has sides that are 1.0 mm long? (b) How many kilometers of beaches in length would this cover if the beach averages 100 m in width and 10.0 m in depth? Neglect air spaces between grains.

10: An expensive vacuum system can achieve a pressure as low as $1.00 \times 10^{- 7} {N/m}^{2}$ at $20^{0} C .$ How many atoms are there in a cubic centimeter at this pressure and temperature?

11: The number density of gas atoms at a certain location in the space above our planet is about $1.00 \times 10^{11} m^{- 3},$ and the pressure is $2.75 \times 10^{- 10} {N/m}^{2}$ in this space. What is the temperature there?

12: A bicycle tire has a pressure of $7.00 \times 10^{5} {N/m}^{2}$ at a temperature of ${18.0}^{0} C$ and contains 2.00 L of gas. What will its pressure be if you let out an amount of air that has a volume of $100 {cm}^{3}$ at atmospheric pressure? Assume tire temperature and volume remain constant.

13: A high-pressure gas cylinder contains 50.0 L of toxic gas at a pressure of $1.40 \times 10^{7} {N/m}^{2}$ and a temperature of ${25.0}^{0} C .$ Its valve leaks after the cylinder is dropped. The cylinder is cooled to dry ice temperature $(- {78.5}^{0} C)$ to reduce the leak rate and pressure so that it can be safely repaired. (a) What is the final pressure in the tank, assuming a negligible amount of gas leaks while being cooled and that there is no phase change? (b) What is the final pressure if one-tenth of the gas escapes? (c) To what temperature must the tank be cooled to reduce the pressure to 1.00 atm (assuming the gas does not change phase and that there is no leakage during cooling)? (d) Does cooling the tank appear to be a practical solution?

14: Find the number of moles in 2.00 L of gas at ${35.0}^{0} C$ and under $7.41 \times 10^{7} {N/m}^{2}$ of pressure.

15: Calculate the depth to which Avogadro’s number of table tennis balls would cover Earth. Each ball has a diameter of 3.75 cm. Assume the space between balls adds an extra 25.0% to their volume and assume they are not crushed by their own weight.

16: (a) What is the gauge pressure in a ${25.0}^{0} C$ car tire containing 3.60 mol of gas in a 30.0 L volume? (b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and ${25.0}^{0} C ?$ Assume the temperature returns to ${25.0}^{0} C$ and the volume remains constant.

17: (a) In the deep space between galaxies, the density of atoms is as low as $10^{6} {atoms/m}^{3},$ and the temperature is a frigid 2.7 K. What is the pressure? (b) What volume (in $m^{3}$ ) is occupied by 1 mol of gas? (c) If this volume is a cube, what is the length of its sides in kilometers?

Glossary

ideal gas law: the physical law that relates the pressure and volume of a gas to the number of gas molecules or number of moles of gas and the temperature of the gas

Boltzmann constant: $k,$ a physical constant that relates energy to temperature; $k = 1.38 \times 10^{- 23} J/K$

Avogadro’s number: $N_{A},$ the number of molecules or atoms in one mole of a substance;
$N_{A} = 6.02 \times 10^{23}$ particles/mole

mole: the quantity of a substance whose mass (in grams) is equal to its molecular mass

Solutions

Check Your Understanding 1

We first need to calculate the molar mass (the mass of one mole) of acetaminophen. To do this, we need to multiply the number of atoms of each element by the element’s atomic mass.

\begin{array}{l} (8 moles of carbon) (12 grams/mole) + (9 moles hydrogen) (1 gram/mole) \\ + (1 mole nitrogen) (14 grams/mole) + (2 moles oxygen) (16 grams/mole) = 151 g \end{array}

Then we need to calculate the number of moles in 325 mg.

(\frac{325 mg}{151 grams/mole}) (\frac{1 gram}{1000 mg})

= 2.15 \times 10^{- 3} moles

Then use Avogadro’s number to calculate the number of molecules.

N = (2.15 \times 10^{- 3} moles) (6.02 \times 10^{23} molecules/mole) = 1.30 \times 10^{21} molecules

Check Your Understanding 2

The best way to approach this question is to think about what is happening. If the density drops to half its original value and no molecules are lost, then the volume must double. If we look at the equation $P V = N k T,$ we see that when the temperature is constant, the pressure is inversely proportional to volume. Therefore, if the volume doubles, the pressure must drop to half its original value, and $P_{f} = 0.50 atm .$

Check Your Understanding 3

Atoms and molecules are close together in solids and liquids. In gases they are separated by empty space. Thus gases have lower densities than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body (such as a sphere) cubed. So if the distance between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1000, and the density decreases by a factor of 1000.

Problems & Exercises

1:

1.62 atm

3:

(a) 0.136 atm

(b) 0.135 atm. The difference between this value and the value from part (a) is negligible.

5:

(a) $n R T = (mol) (J/mol \cdot K) (K) = J$

(b) $n R T = (mol) (cal/mol \cdot K) (K) = cal$

(c) $\begin{array}{ll} n R T & = (mol) (L \cdot atm/mol \cdot K) (K) \\ = L \cdot atm = (m^{3}) ({N/m}^{2}) \\ = N \cdot m = J \end{array}$

7:

$7.86 \times 10^{- 2} mol$

9:

(a) $6.02 \times 10^{5} {km}^{3}$

(b) $6.02 \times 10^{8} km$

11:

$- {73.9}^{0} C$

13:

(a) $9.14 \times 10^{6} {N/m}^{2}$

(b) $8.23 \times 10^{6} {N/m}^{2}$

(c) 2.16 K

(d) No. The final temperature needed is much too low to be easily achieved for a large object.

15:

41 km

17:

(a) $3.7 \times 10^{- 17} Pa$

(b) $6.0 \times 10^{17} m^{3}$

(c) $8.4 \times 10^{2} km$

License

Icon for the Creative Commons Attribution 4.0 International License

Summary

IDEAL GAS LAW

Example 1: Calculating Pressure Changes Due to Temperature Changes: Tire Pressure

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT—REFRIGERATING A BALLOON

Example 2: Calculating the Number of Molecules in a Cubic Meter of Gas

Moles and Avogadro’s Number

AVOGADRO’S NUMBER

Check Your Understanding 1

Example 3: Calculating Moles per Cubic Meter and Liters per Mole

Check Your Understanding 2

The Ideal Gas Law Restated Using Moles

IDEAL GAS LAW (IN TERMS OF MOLES)

Example 4: Calculating Number of Moles: Gas in a Bike Tire

The Ideal Gas Law and Energy

PROBLEM-SOLVING STRATEGY: THE IDEAL GAS LAW

Check Your Understanding 3

Section Summary

Conceptual Questions

Problems & Exercises

Glossary

Solutions

License

Share This Book