40 6.6 Satellites and Kepler’s Laws: An Argument for Simplicity

Summary

  • State Kepler’s laws of planetary motion.
  • Derive the third Kepler’s law for circular orbits.
  • Discuss the Ptolemaic model of the universe.

Examples of gravitational orbits abound. Hundreds of artificial satellites orbit Earth together with thousands of pieces of debris. The Moon’s orbit about Earth has intrigued humans from time immemorial. The orbits of planets, asteroids, meteors, and comets about the Sun are no less interesting. If we look further, we see almost unimaginable numbers of stars, galaxies, and other celestial objects orbiting one another and interacting through gravity.

All these motions are governed by gravitational force, and it is possible to describe them to various degrees of precision. Precise descriptions of complex systems must be made with large computers. However, we can describe an important class of orbits without the use of computers, and we shall find it instructive to study them. These orbits have the following characteristics:

  1. A small mass [latex]{m}[/latex] orbits a much larger mass [latex]{M}.[/latex] This allows us to view the motion as if [latex]{M}[/latex] were stationary—in fact, as if from an inertial frame of reference placed on [latex]{M}[/latex] —without significant error. Mass [latex]{m}[/latex] is the satellite of [latex]{M},[/latex] if the orbit is gravitationally bound.
  2. The system is isolated from other masses. This allows us to neglect any small effects due to outside masses.

The conditions are satisfied, to good approximation, by Earth’s satellites (including the Moon), by objects orbiting the Sun, and by the satellites of other planets. Historically, planets were studied first, and there is a classical set of three laws, called Kepler’s laws of planetary motion, that describe the orbits of all bodies satisfying the two previous conditions (not just planets in our solar system). These descriptive laws are named for the German astronomer Johannes Kepler (1571–1630), who devised them after careful study (over some 20 years) of a large amount of meticulously recorded observations of planetary motion done by Tycho Brahe (1546–1601). Such careful collection and detailed recording of methods and data are hallmarks of good science. Data constitute the evidence from which new interpretations and meanings can be constructed.

Kepler’s Laws of Planetary Motion

Kepler’s First Law

The orbit of each planet about the Sun is an ellipse with the Sun at one focus.

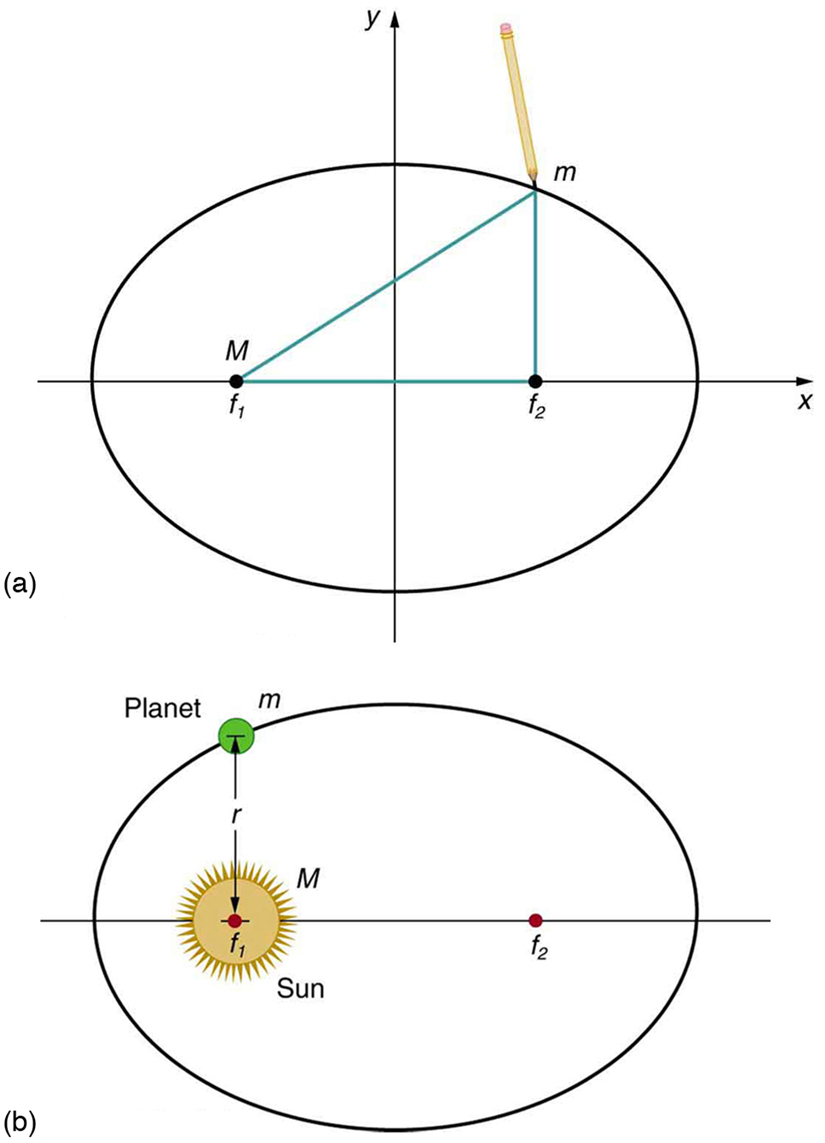
In figure a, an ellipse is shown on the coordinate axes. Two foci of the ellipse are joined to a point m on the ellipse. A pencil is shown at the point m. In figure b the elliptical path of a planet is shown. At the left focus f-one of the path the Sun is shown. The planet is shown just above the Sun on the elliptical path.
Figure 1. (a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci ( f1 and f2) is a constant. You can draw an ellipse as shown by putting a pin at each focus, and then placing a string around a pencil and the pins and tracing a line on paper. A circle is a special case of an ellipse in which the two foci coincide (thus any point on the circle is the same distance from the center). (b) For any closed gravitational orbit, m follows an elliptical path with M at one focus. Kepler’s first law states this fact for planets orbiting the Sun.

Kepler’s Second Law

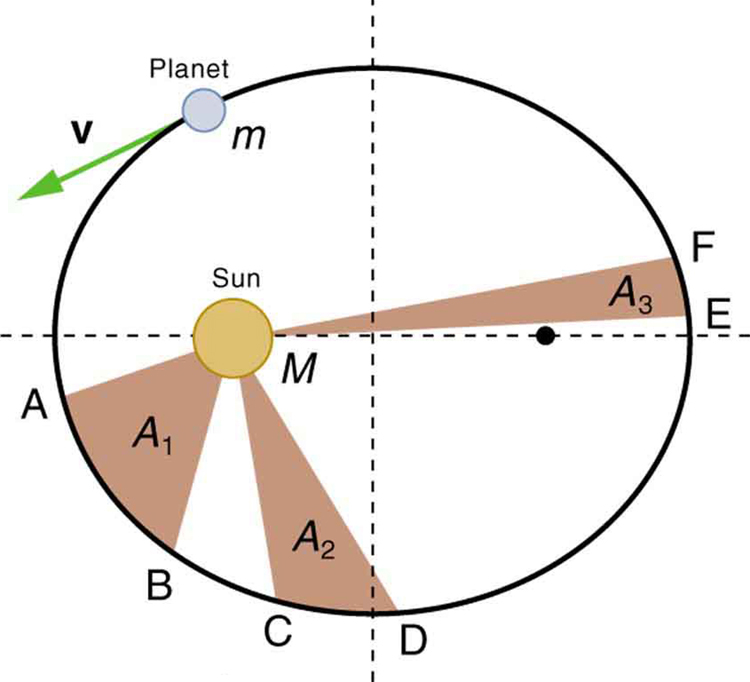
Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal times (see Figure 2).

Kepler’s Third Law

The ratio of the squares of the periods of any two planets about the Sun is equal to the ratio of the cubes of their average distances from the Sun. In equation form, this is

[latex]{\frac{T_1^2}{T_2^2}}[/latex] [latex]{=}[/latex] [latex]{\frac{r_1^3}{r_2^3}},[/latex]

where [latex]{T}[/latex] is the period (time for one orbit) and [latex]{r}[/latex] is the average radius. This equation is valid only for comparing two small masses orbiting the same large one. Most importantly, this is a descriptive equation only, giving no information as to the cause of the equality.

In the figure, the elliptical path of a planet is shown. The Sun is at the left focus. Three shaded regions M A B, M C D and M E F are marked on the figure by joining the Sun to the three pairs of points A B, C D, and E F on the elliptical path. The velocity of the planet is shown on the planet in a direction tangential to the path.
Figure 2. The shaded regions have equal areas. It takes equal times for m to go from A to B, from C to D, and from E to F. The mass m moves fastest when it is closest to M. Kepler’s second law was originally devised for planets orbiting the Sun, but it has broader validity.

Note again that while, for historical reasons, Kepler’s laws are stated for planets orbiting the Sun, they are actually valid for all bodies satisfying the two previously stated conditions.

Example 1: Find the Time for One Orbit of an Earth Satellite

Given that the Moon orbits Earth each 27.3 d and that it is an average distance of [latex]{3.84\times10^8\text{ m}}[/latex] from the center of Earth, calculate the period of an artificial satellite orbiting at an average altitude of 1500 km above Earth’s surface.

Strategy

The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form in [latex]{\frac{T_1^2}{T_2^2}=\frac{r_1^3}{r_2^3}}.[/latex] Let us use the subscript 1 for the Moon and the subscript 2 for the satellite. We are asked to find [latex]{T_2}.[/latex] The given information tells us that the orbital radius of the Moon is [latex]{r_1=3.84\times10^8\text{ m}},[/latex] and that the period of the Moon is [latex]{T_1=27.3\text{ d}}.[/latex] The height of the artificial satellite above Earth’s surface is given, and so we must add the radius of Earth (6380 km) to get [latex]{r_2=(1500+6380)\text{ km}=7880\text{ km}}.[/latex] Now all quantities are known, and so [latex]{T_2}[/latex] can be found.

Solution

Kepler’s third law is

[latex]{\frac{T_1^2}{T_2^2}}[/latex] [latex]{=}[/latex] [latex]{\frac{r_1^3}{r_2^3}}.[/latex]

To solve for [latex]{T_2},[/latex] we cross-multiply and take the square root, yielding

[latex]{T_2^2=T_1^2}[/latex] [latex]{(\frac{r_2}{r_1})^3}[/latex]
[latex]{T_2=T_1}[/latex] [latex]{(\frac{r_2}{r_1})^{3/2}}.[/latex]

Substituting known values yields

[latex]\begin{array}{lcl} {T_2} & = & {27.3\text{ d}\times\frac{24.0\text{ h}}{\text{d}}\times(\frac{7880\text{ km}}{3.84\times10^5\text{ km}})^{3/2}} \\ {} & = & {1.93\text{ h}} \end{array}[/latex]

Discussion This is a reasonable period for a satellite in a fairly low orbit. It is interesting that any satellite at this altitude will orbit in the same amount of time. This fact is related to the condition that the satellite’s mass is small compared with that of Earth.

People immediately search for deeper meaning when broadly applicable laws, like Kepler’s, are discovered. It was Newton who took the next giant step when he proposed the law of universal gravitation. While Kepler was able to discover what was happening, Newton discovered that gravitational force was the cause.

Derivation of Kepler’s Third Law for Circular Orbits

We shall derive Kepler’s third law, starting with Newton’s laws of motion and his universal law of gravitation. The point is to demonstrate that the force of gravity is the cause for Kepler’s laws (although we will only derive the third one).

Let us consider a circular orbit of a small mass [latex]{m}[/latex] around a large mass [latex]{M},[/latex] satisfying the two conditions stated at the beginning of this section. Gravity supplies the centripetal force to mass [latex]{m}.[/latex] Starting with Newton’s second law applied to circular motion,

[latex]{F_{\text{net}}=ma_{\text{c}}=m}[/latex] [latex]{\frac{v^2}{r}}.[/latex]

The net external force on mass [latex]{m}[/latex] is gravity, and so we substitute the force of gravity for [latex]{F_{\text{net}}}:[/latex]

[latex]{G}[/latex] [latex]{\frac{mM}{r^2}}[/latex] [latex]{=m}[/latex] [latex]{\frac{v^2}{r}}.[/latex]

The mass [latex]{m}[/latex] cancels, yielding

[latex]{G}[/latex] [latex]{\frac{M}{r}}[/latex] [latex]{=\:v^2}.[/latex]

The fact that [latex]{m}[/latex] cancels out is another aspect of the oft-noted fact that at a given location all masses fall with the same acceleration. Here we see that at a given orbital radius [latex]{r},[/latex] all masses orbit at the same speed. (This was implied by the result of the preceding worked example.) Now, to get at Kepler’s third law, we must get the period [latex]{T}[/latex] into the equation. By definition, period [latex]{T}[/latex] is the time for one complete orbit. Now the average speed [latex]{v}[/latex] is the circumference divided by the period—that is,

[latex]{v\:=}[/latex] [latex]{\frac{2\pi{r}}{T}}.[/latex]

Substituting this into the previous equation gives

[latex]{G}[/latex] [latex]{\frac{M}{r}}[/latex] [latex]{=}[/latex] [latex]{\frac{4\pi^2r^2}{T^2}}.[/latex]

Solving for [latex]{T^2}[/latex] yields

[latex]{T^2\:=}[/latex] [latex]{\frac{4\pi^2}{GM}}[/latex] [latex]{r^3}.[/latex]

Using subscripts 1 and 2 to denote two different satellites, and taking the ratio of the last equation for satellite 1 to satellite 2 yields

[latex]{\frac{T_1^2}{T_2^2}}[/latex] [latex]{=}[/latex] [latex]{\frac{r_1^3}{r_2^3}}.[/latex]

This is Kepler’s third law. Note that Kepler’s third law is valid only for comparing satellites of the same parent body, because only then does the mass of the parent body [latex]{M}[/latex] cancel.

Now consider what we get if we solve [latex]{T^2=\frac{4\pi^2}{GM}r^3}.[/latex] We obtain a relationship that can be used to determine the mass [latex]{M}[/latex] of a parent body from the orbits of its satellites:

[latex]{\frac{r^3}{T^2}}[/latex] [latex]{=}[/latex] [latex]{\frac{G}{4\pi^2}}[/latex] [latex]{M}.[/latex]

If [latex]{r}[/latex] and [latex]{T}[/latex] are known for a satellite, then the mass [latex]{M}[/latex] of the parent can be calculated. This principle has been used extensively to find the masses of heavenly bodies that have satellites. Furthermore, the ratio [latex]{r^3{/}T^2}[/latex] should be a constant for all satellites of the same parent body (because [latex]{r^3{/}T^2=GM{/}4\pi^2}[/latex] ). (See Table 2).

It is clear from Table 2 that the ratio of [latex]{r^3{/}T^2}[/latex] is constant, at least to the third digit, for all listed satellites of the Sun, and for those of Jupiter. Small variations in that ratio have two causes—uncertainties in the [latex]{r}[/latex] and [latex]{T}[/latex] data, and perturbations of the orbits due to other bodies. Interestingly, those perturbations can be—and have been—used to predict the location of new planets and moons. This is another verification of Newton’s universal law of gravitation.

MAKING CONNECTIONS

Newton’s universal law of gravitation is modified by Einstein’s general theory of relativity, as we shall see in Chapter 33 Particle Physics. Newton’s gravity is not seriously in error—it was and still is an extremely good approximation for most situations. Einstein’s modification is most noticeable in extremely large gravitational fields, such as near black holes. However, general relativity also explains such phenomena as small but long-known deviations of the orbit of the planet Mercury from classical predictions.

The Case for Simplicity

The development of the universal law of gravitation by Newton played a pivotal role in the history of ideas. While it is beyond the scope of this text to cover that history in any detail, we note some important points. The definition of planet set in 2006 by the International Astronomical Union (IAU) states that in the solar system, a planet is a celestial body that:

  1. is in orbit around the Sun,
  2. has sufficient mass to assume hydrostatic equilibrium and
  3. has cleared the neighborhood around its orbit.

A non-satellite body fulfilling only the first two of the above criteria is classified as “dwarf planet.”

In 2006, Pluto was demoted to a ‘dwarf planet’ after scientists revised their definition of what constitutes a “true” planet.

Parent Satellite Average orbital radius r(km) Period T(y) r3 / T2 (km3 / y2)
Earth Moon [latex]{3.84\times10^5}[/latex] 0.07481 [latex]{1.01\times10^{19}}[/latex]
Sun Mercury [latex]{5.79\times10^7}[/latex] 0.2409 [latex]{3.34\times10^{24}}[/latex]
Venus [latex]{1.082\times10^8}[/latex] 0.6150 [latex]{3.35\times10^{24}}[/latex]
Earth [latex]{1.496\times10^8}[/latex] 1.000 [latex]{3.35\times10^{24}}[/latex]
Mars [latex]{2.279\times10^8}[/latex] 1.881 [latex]{3.35\times10^{24}}[/latex]
Jupiter [latex]{7.783\times10^8}[/latex] 11.86 [latex]{3.35\times10^{24}}[/latex]
Saturn [latex]{1.427\times10^9}[/latex] 29.46 [latex]{3.35\times10^{24}}[/latex]
Neptune [latex]{4.497\times10^9}[/latex] 164.8 [latex]{3.35\times10^{24}}[/latex]
Pluto [latex]{5.90\times10^9}[/latex] 248.3 [latex]{3.33\times10^{24}}[/latex]
Jupiter Io [latex]{4.22\times10^5}[/latex] 0.00485 (1.77 d) [latex]{3.19\times10^{21}}[/latex]
Europa [latex]{6.71\times10^5}[/latex] 0.00972 (3.55 d) [latex]{3.20\times10^{21}}[/latex]
Ganymede [latex]{1.07\times10^6}[/latex] 0.0196 (7.16 d) [latex]{3.19\times10^{21}}[/latex]
Callisto [latex]{1.88\times10^6}[/latex] 0.0457 (16.19 d) [latex]{3.20\times10^{21}}[/latex]
Table 2. Orbital Data and Kepler’s Third Law.

The universal law of gravitation is a good example of a physical principle that is very broadly applicable. That single equation for the gravitational force describes all situations in which gravity acts. It gives a cause for a vast number of effects, such as the orbits of the planets and moons in the solar system. It epitomizes the underlying unity and simplicity of physics.

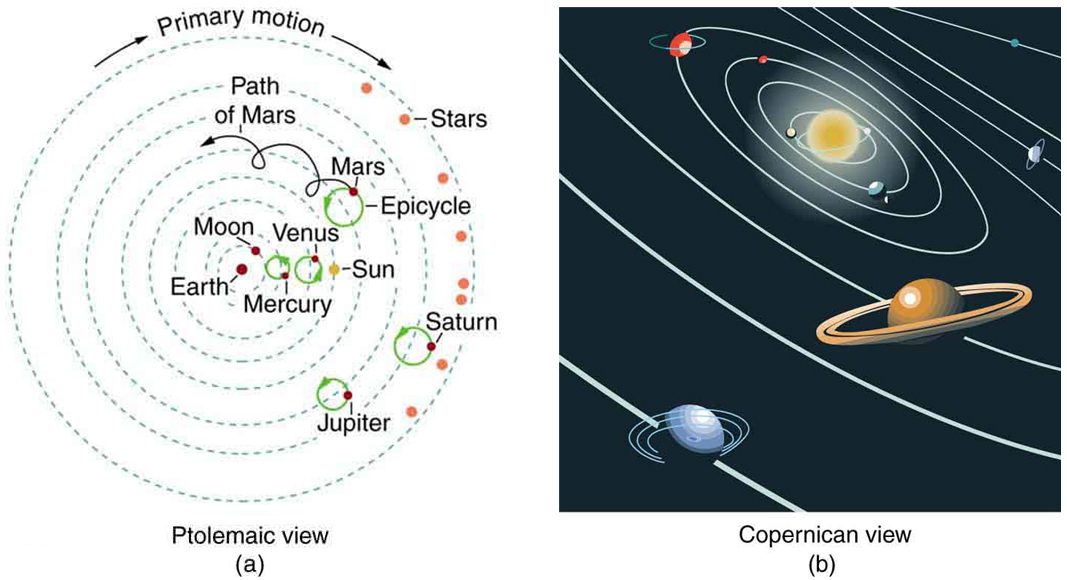
Before the discoveries of Kepler, Copernicus, Galileo, Newton, and others, the solar system was thought to revolve around Earth as shown in Figure 3(a). This is called the Ptolemaic view, for the Greek philosopher who lived in the second century AD. This model is characterized by a list of facts for the motions of planets with no cause and effect explanation. There tended to be a different rule for each heavenly body and a general lack of simplicity.

Figure 3(b) represents the modern or Copernican model. In this model, a small set of rules and a single underlying force explain not only all motions in the solar system, but all other situations involving gravity. The breadth and simplicity of the laws of physics are compelling. As our knowledge of nature has grown, the basic simplicity of its laws has become ever more evident.

In figure a the paths of the different planets are shown in the forms of dotted concentric circles with the Earth at the center with its Moon. The Sun is also shown revolving around the Earth. Each planet is labeled with its name. On the planets Mercury, Venus, Mars, Jupiter and Saturn green colored epicycles are shown. In the figure b Copernican view of planet is shown. The Sun is shown at the center of the solar system. The planets are shown moving around the Sun.
Figure 3. (a) The Ptolemaic model of the universe has Earth at the center with the Moon, the planets, the Sun, and the stars revolving about it in complex superpositions of circular paths. This geocentric model, which can be made progressively more accurate by adding more circles, is purely descriptive, containing no hints as to what are the causes of these motions. (b) The Copernican model has the Sun at the center of the solar system. It is fully explained by a small number of laws of physics, including Newton’s universal law of gravitation.

Section Summary

  • Kepler’s laws are stated for a small mass [latex]{m}[/latex] orbiting a larger mass [latex]{M}[/latex] in near-isolation. Kepler’s laws of planetary motion are then as follows:

    Kepler’s first law

    The orbit of each planet about the Sun is an ellipse with the Sun at one focus.

    Kepler’s second law

    Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal times.

    Kepler’s third law

    The ratio of the squares of the periods of any two planets about the Sun is equal to the ratio of the cubes of their average distances from the Sun:

    [latex]{\frac{T_1^2}{T_2^2}}[/latex] [latex]{=}[/latex] [latex]{\frac{r_1^3}{r_2^3}},[/latex]

    where [latex]{T}[/latex] is the period (time for one orbit) and rr size 12{m} {} is the average radius of the orbit.

  • The period and radius of a satellite’s orbit about a larger body [latex]{M}[/latex] are related by
    [latex]{T_2\:=}[/latex] [latex]{\frac{4\pi^2}{GM}}[/latex] [latex]{r^3}[/latex]

    or

    [latex]{\frac{r^3}{T^2}}[/latex] [latex]{=}[/latex] [latex]{\frac{G}{4\pi^2}}[/latex] [latex]{M}.[/latex]

Conceptual Questions

1: In what frame(s) of reference are Kepler’s laws valid? Are Kepler’s laws purely descriptive, or do they contain causal information?

Problems & Exercises

1: A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth’s rotation). Calculate the radius of such an orbit based on the data for the moon in Table 2.

2: Calculate the mass of the Sun based on data for Earth’s orbit and compare the value obtained with the Sun’s actual mass.

3: Find the mass of Jupiter based on data for the orbit of one of its moons, and compare your result with its actual mass.

4: Find the ratio of the mass of Jupiter to that of Earth based on data in Table 2.

5: Astronomical observations of our Milky Way galaxy indicate that it has a mass of about [latex]{8.0\times10^{11}}[/latex] solar masses. A star orbiting on the galaxy’s periphery is about [latex]{6.0\times10^4}[/latex] light years from its center. (a) What should the orbital period of that star be? (b) If its period is [latex]{6.0\times10^7}[/latex] instead, what is the mass of the galaxy? Such calculations are used to imply the existence of “dark matter” in the universe and have indicated, for example, the existence of very massive black holes at the centers of some galaxies.

6: Integrated Concepts

Space debris left from old satellites and their launchers is becoming a hazard to other satellites. (a) Calculate the speed of a satellite in an orbit 900 km above Earth’s surface. (b) Suppose a loose rivet is in an orbit of the same radius that intersects the satellite’s orbit at an angle of [latex]{90^0}[/latex] relative to Earth. What is the velocity of the rivet relative to the satellite just before striking it? (c) Given the rivet is 3.00 mm in size, how long will its collision with the satellite last? (d) If its mass is 0.500 g, what is the average force it exerts on the satellite? (e) How much energy in joules is generated by the collision? (The satellite’s velocity does not change appreciably, because its mass is much greater than the rivet’s.)

7: Unreasonable Results

(a) Based on Kepler’s laws and information on the orbital characteristics of the Moon, calculate the orbital radius for an Earth satellite having a period of 1.00 h. (b) What is unreasonable about this result? (c) What is unreasonable or inconsistent about the premise of a 1.00 h orbit?

8: Construct Your Own Problem

On February 14, 2000, the NEAR spacecraft was successfully inserted into orbit around Eros, becoming the first artificial satellite of an asteroid. Construct a problem in which you determine the orbital speed for a satellite near Eros. You will need to find the mass of the asteroid and consider such things as a safe distance for the orbit. Although Eros is not spherical, calculate the acceleration due to gravity on its surface at a point an average distance from its center of mass. Your instructor may also wish to have you calculate the escape velocity from this point on Eros.

 

Solutions

Problems & Exercises

2:

[latex]{1.98\times10^{30}\text{ kg}}[/latex]

4:

[latex]{\frac{M_{\text{J}}}{M_{\text{E}}}=316}[/latex]

6:

a) [latex]{7.4\times10^3\text{ m/s}}[/latex]

b) [latex]{1.05\times10^3\text{ m/s}}[/latex]

c) [latex]{2.86\times10^{-7}\text{ s}}[/latex]

d) [latex]{1.84\times10^7\text{ N}}[/latex]

e) [latex]{2.76\times10^4\text{ J}}[/latex]

7:

a) [latex]{5.08\times10^3\text{ km}}[/latex]

b) This radius is unreasonable because it is less than the radius of earth.

c) The premise of a one-hour orbit is inconsistent with the known radius of the earth.

 

License

Icon for the Creative Commons Attribution 4.0 International License

College Physics Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book